Learning Zone, OHM Academy- Dalam artikel learning zone ini, kami akan memberikan strategi ampuh dalam menaklukkan soal untuk siswa SMP yang akan menghadapi TKA Matematika diwaktu yang akan datang.
Apa Itu TKA Matematika?
Tes Kemampuan Akademik (TKA) tingkat SMP merupakan evaluasi yang dirancang untuk mengukur kemampuan akademik siswa secara objektif, bukan sebagai penentu kelulusan. Melalui TKA, sekolah dapat memperoleh gambaran menyeluruh tentang kekuatan dan kelemahan belajar setiap siswa. Hasilnya juga menjadi pertimbangan penting dalam proses seleksi ke jenjang pendidikan berikutnya. Lebih dari itu, pelaksanaan TKA bertujuan untuk menyetarakan hasil belajar antara pendidikan formal dan nonformal, sekaligus membantu sekolah dalam meningkatkan kualitas proses pembelajaran dan layanan pendidikannya.
TKA Matematika tingkat SMP menuntut tidak hanya kemampuan menghitung, tetapi juga penguasaan konsep, kecepatan, dan strategi pengerjaan yang tepat. Dengan memahami materi utama, mengenali tipe soal, serta menerapkan teknik pengerjaan yang efisien, siswa dapat meningkatkan peluang meraih hasil optimal. Sebagaimana disebut oleh Pusat Asesmen Pendidikan (Pusmendik) – Kemdikbud: “Kerjakan soal yang mudah terlebih dahulu … jangan kehabisan waktu di soal sulit.”
Bagaimana Strategi Agar Dapat Tembus Ujian TKA?
Kenali Materi dan Kisi-Kisi dengan Baik
Langkah awal dalam mempersiapkan diri menghadapi TKA Matematika SMP adalah memahami materi yang akan diujikan serta kisi-kisi soal yang menjadi acuannya. Dengan mengenali cakupan materi sejak awal, peserta dapat belajar secara terarah dan menyesuaikan strategi belajar sesuai kebutuhan.
Berdasarkan penjelasan dari Kementerian Pendidikan, Kebudayaan, Riset, dan Teknologi (Kemdikbud), TKA Matematika pada jenjang SMP/MTs/sederajat dirancang untuk mengukur kemampuan siswa dalam memahami fakta, konsep, dan prinsip matematika, serta kemampuan menerapkannya dalam pemecahan masalah kontekstual.
- Langkah-langkah yang dapat dilakukan:
- Mempelajari kisi-kisi resmi atau meminta informasi dari guru mengenai topik-topik yang akan diujikan.
- Menguasai seluruh materi pokok yang biasanya muncul dalam ujian, seperti bilangan, aljabar dasar, geometri dan pengukuran, serta data dan peluang.
- Menyusun daftar penguasaan materi pribadi, yaitu dengan menandai topik yang sudah dikuasai dan topik yang masih perlu diperdalam.
Melalui langkah-langkah tersebut, siswa dapat mempersiapkan diri secara sistematis dan efisien, sehingga kemampuan yang dimiliki dapat digunakan secara optimal saat mengerjakan soal TKA Matematika.
Pahami Konsep, Bukan Sekadar Menghafal Rumus
Salah satu kesalahan yang sering dilakukan oleh peserta ujian adalah terlalu bergantung pada hafalan rumus tanpa memahami dasar logika atau alasan di balik penggunaannya. Pemahaman terhadap konsep merupakan hal yang jauh lebih penting, karena soal-soal TKA Matematika tidak hanya menguji kemampuan menghitung, tetapi juga kemampuan menalar dan menerapkan konsep matematika dalam situasi yang berbeda.
Mengapa pemahaman konsep lebih penting? Dalam TKA, banyak soal yang disajikan dengan konteks baru atau bentuk penyajian yang berbeda dari contoh yang biasa dipelajari. Jika siswa hanya menghafal rumus, mereka akan kesulitan menyesuaikan diri dengan variasi soal tersebut. Sebaliknya, siswa yang memahami konsep dasar dapat menyesuaikan cara berpikir dan menemukan solusi secara logis, meskipun soal disajikan dengan cara yang tidak biasa
Langkah-langkah yang dapat dilakukan:
- Pelajari makna di balik rumus.
Misalnya, pada materi persamaan linear satu variabel (ax + b = 0), pahami mengapa solusi diperoleh dengan x=− . Dengan memahami proses perhitungan tersebut, siswa akan mengerti hubungan antara koefisien dan nilai variabel, bukan sekadar mengingat hasil akhirnya. - Hubungkan konsep dengan kehidupan sehari-hari.
Jika soal menggambarkan permasalahan nyata, seperti jumlah barang atau panjang tali, cobalah menuliskan model matematikanya sendiri agar lebih mudah dipahami. - Latih kemampuan berpikir kritis.
Kerjakan soal yang menuntut penalaran dan pemahaman konsep, bukan hanya soal yang bisa diselesaikan dengan rumus langsung. Dengan demikian, kemampuan berpikir analitis akan terbentuk dan lebih siap menghadapi soal-soal dengan tingkat variasi tinggi.
Latihan Soal Berkualitas dan Evaluasi Diri|
Strategi penting dalam mempersiapkan diri menghadapi TKA Matematika adalah berlatih secara rutin dengan soal-soal berkualitas yang memiliki karakteristik serupa dengan soal ujian sebenarnya. Melalui latihan teratur, siswa dapat mengasah kemampuan berpikir logis, mengenali pola soal, serta meningkatkan ketepatan dan kecepatan dalam menjawab.
Namun, latihan saja tidak cukup. Setelah mengerjakan soal, siswa perlu melakukan evaluasi diri untuk mengetahui sejauh mana pemahamannya terhadap materi. Evaluasi ini membantu mengidentifikasi kelemahan, baik dari segi konsep maupun strategi pengerjaan.
Langkah-langkah yang disarankan:
- Tetapkan jadwal latihan secara konsisten.
Lakukan latihan soal setiap hari atau beberapa kali dalam seminggu selama 30–60 menit per sesi agar kemampuan tetap terasah. - Analisis hasil latihan.
Periksa kembali soal yang salah atau memerlukan waktu lama untuk dikerjakan. Tentukan apakah kesalahan terjadi karena kurang memahami konsep atau karena kurang teliti. - Buat catatan kesalahan pribadi.
Kumpulkan soal-soal yang sulit dalam sebuah “bank kesalahan” (error bank) dan ulangi latihan pada waktu tertentu. Dengan cara ini, siswa dapat memantau perkembangan dan memastikan kesalahan yang sama tidak terulang.
Gunakan Strategi Pengerjaan yang Efisien
Selain penguasaan materi, keberhasilan dalam ujian juga ditentukan oleh strategi pengerjaan soal. Kemampuan mengatur waktu dan menentukan urutan pengerjaan merupakan kunci penting untuk memaksimalkan hasil.
Beberapa strategi yang dapat diterapkan:
- Kerjakan soal yang mudah terlebih dahulu.
Cara ini membantu mengumpulkan poin lebih cepat dan meningkatkan rasa percaya diri di awal ujian. - Atur waktu dengan bijak.
Jika suatu soal memerlukan waktu lama, lewati terlebih dahulu dan lanjutkan ke soal berikutnya. Kembali lagi jika waktu masih tersisa. - Sediakan waktu untuk memeriksa ulang.
Pastikan ada waktu di akhir ujian untuk meninjau kembali jawaban, terutama pada soal perhitungan yang rawan kesalahan. - Pertimbangkan sistem penilaian.
Jika sistem ujian tidak memberikan pengurangan nilai untuk jawaban salah, siswa disarankan tetap memberikan jawaban meskipun ragu, agar peluang memperoleh poin tetap ada.
Bangun Kebiasaan Belajar dan Sikap Positif
Selain kemampuan akademik, kesiapan mental dan kebiasaan belajar yang baik juga berpengaruh besar terhadap hasil ujian. Sikap positif membantu siswa tetap fokus dan percaya diri saat menghadapi tekanan ujian.
Langkah yang dapat dilakukan:
- Susun jadwal belajar yang realistis dan teratur.
Dengan jadwal yang konsisten, proses belajar menjadi lebih efektif dan tidak menumpuk menjelang ujian. - Tumbuhkan rasa percaya diri.
Yakinkan diri bahwa setiap usaha belajar akan membawa hasil. Hindari rasa takut terhadap soal sulit, dan anggap kesulitan sebagai tantangan untuk berkembang. - Kendalikan stres menjelang ujian.
Lakukan teknik relaksasi ringan, seperti menarik napas dalam atau mendengarkan musik tenang, agar pikiran lebih fokus dan tenang.
Revisi Akhir dan Simulasi Ujian
Menjelang hari pelaksanaan TKA, siswa disarankan untuk melakukan simulasi ujian guna melatih ketahanan waktu, konsentrasi, dan manajemen stres selama ujian berlangsung.
Langkah-langkah simulasi yang efektif:
- Lakukan simulasi dengan kondisi menyerupai ujian sebenarnya.
Atur waktu pengerjaan, suasana tenang, dan hindari penggunaan alat bantu apa pun selain yang diperbolehkan. - Gunakan sumber latihan yang kredibel.
Manfaatkan soal-soal dari uji coba (try-out) atau kumpulan soal TKA tahun sebelumnya sebagai bahan latihan. - Evaluasi hasil simulasi secara objektif.
Catat jenis soal yang masih sulit, kemudian fokuskan waktu belajar tambahan pada bagian tersebut agar kelemahan dapat diminimalkan.
Melalui simulasi dan evaluasi akhir, siswa dapat menyesuaikan strategi belajar sekaligus meningkatkan kesiapan menghadapi ujian dengan lebih percaya diri
Lalu, Elemen Apa Saja yang Diujikan dalam TKA Matematika SMP?
Elemen ini berdasarkan pola soal yang tercantum dalam web resmi Kemendikbudristek berikut ini merupakan kompetensi yang perlu dipersiapkan:
| No | Elemen/ Materi | Sub Materi | Kompetensi | Batasan/ Catatan |
| Bilangan | Bilangan Real | Memahami, mengaplikasikan, dan bernalar yang lebih tinggi untuk menyelesaikan permasalahan terkait cakupan sub-elemen berikut: Perbandingan dan sifat-sifat bilangan;Operasi aritmetika pada bilangan;Estimasi/ perkiraan hasil perhitungan;Faktorisasi prima bilangan asli;Rasio (skala, proporsi, dan laju perubahan);Perbandingan senilai dan berbalik nilai. | Bilangan mencakup berbagai jenis bilangan yang meliputi bilangan bulat, bilangan rasional dan irasional, bilangan berpangkat bulat, bilangan akar, serta bilangan yang dinyatakan dalam notasi ilmiah. | |
| Aljabar | Persamaan dan ketidaksamaan linier | Peserta diharapkan dapat Menguasai, menerapkan, dan menalar secara mendalam untuk menyelesaikan berbagai permasalahan yang berkaitan dengan cakupan sub-elemen berikut: Persamaan linear satu variabel;Pertidaksamaanlinear satu variabel; Sistem persamaan linear dua variabel. | . | |
| Bentuk Aljabar | Menguasai kemampuan memahami, mengaplikasikan, dan menalar secara mendalam dalam memecahkan berbagai permasalahan yang mencakup sub-elemen berikut: Bentuk aljabar dan sifat-sifat operasinya (komutatif, asosiatif, dan distributif). | |||
| Fungsi | Memahami, menerapkan, dan menalar pada tingkat yang lebih tinggi dalam menyelesaikan permasalahan yang berkaitan dengan cakupan sub-elemen berikut: Relasi dan fungsi (domain, kodomain, range), serta penyajiannya. | |||
| Barisan dan Deret | Memahami, menerapkan, dan menalar pada tingkat yang lebih tinggi dalam menyelesaikan permasalahan yang berkaitan dengan cakupan sub-elemen berikut: Barisan berhingga bilanganDeret berhingga bilangan | |||
| Geometri dan Pengukuran | Objek Geometri | Kemampuan untuk memahami, mengaplikasikan, dan menalar secara logis dalam memecahkan masalah yang meliputi: Hubungan antar-sudut pada dua garis yang berpotongan serta dua garis sejajar yang dipotong garis transversal, termasuk menentukan besar sudut pada segitiga;Penerapan Teorema Pythagoras dalam berbagai situasi;Kekongruenan dan kesebangunan pada bangun datar;Jaring-jaring berbagai bangun ruang, seperti prisma, tabung, limas, dan kerucut. | ||
| Transformasi Geometri | Kemampuan untuk memahami, mengaplikasikan, dan menalar secara logis dalam menyelesaikan permasalahan yang berkaitan dengan transformasi tunggal, seperti refleksi, translasi, rotasi, dan dilatasi, baik pada titik, garis, maupun bangun datar di bidang. | |||
| Pengukuran | Kemampuan untuk memahami, mengaplikasikan, dan menalar secara mendalam dalam memecahkan permasalahan terkait: penghitungan keliling dan luas pada bangun datar (segi-banyak, lingkaran, dan kombinasi daerah);penentuan volume bangun ruang seperti prisma, limas, dan bola. | |||
| Data dan Peluang | Data | Kemampuan untuk memahami, mengaplikasikan, dan menalar secara logis dalam memecahkan permasalahan yang berkaitan dengan: merumuskan pertanyaan untuk memperoleh data, serta menyajikan dan menafsirkan hasilnya;menentukan dan memperkirakan nilai rerata, median, modus, serta jangkauan suatu data;membandingkan ukuran pemusatan dan penyebaran dari beberapa kelompok data. | Penyajian data dapat dilakukan melalui berbagai cara, seperti diagram batang, diagram garis, diagram lingkaran, serta tabel, agar informasi lebih mudah dibaca dan dipahami. | |
| Peluang | Menguasai, menerapkan, Kemampuan untuk memahami dan mengaplikasikan konsep peluang pada kejadian tunggal, serta menghitung dan menafsirkan frekuensi relatif sebagai ukuran probabilitas empiris. |
Sumber: Pusmendik (Pusat Asesmen Pendidikan)
Contoh Soal TKA Matematika dan Pembahasannya:
Soal Nomor : 1
Kompetensi : Memahami, mengaplikasikan, dan bernalar yang lebih tinggi untuk menyelesaikan permasalahan terkait Faktorisasi prima bilangan asli
Terdapat tiga bilangan yang dinyatakan dengan (212 – 122), (182 + 162), dan (42 × 30) Bilangan apa yang merupakan faktor persekutuan ketiga bilangan tersebut?
- 23×32×5
- 22×32×5
- 22×322×
- 32 × 5
- 22 ×3× 5
Jawaban:
Pembahasan:
Hitung masing-masing bilangan:
242−122=(24−12)(24+12)=12×36=432
182+162=324+162=486
42×30=1260
Faktorisasi prima
432
432=24×33
486
486=2×35
1260
1260=22×32×5×7
Tentukan faktor persekutuan (FPB)
| Faktor | 432 | 486 | 1260 | Pangkat terkecil |
| 2 | 4 | 1 | 2 | 1 |
| 3 | 3 | 5 | 2 | 2 |
| 5 | – | – | 1 | – |
| 7 | – | – | 1 | – |
FPB = 21 × 3² = 18
Jadi faktor persekutuan ketiganya adalah 18 → 2×32.
Soal Nomor : 2
Kompetensi : Memahami, mengaplikasikan, dan bernalar yang lebih tinggi untuk menyelesaikan permasalahan terkait perbandingan senilai dan berbalik nilai
Harga 1 kilogram ikan tenggiri adalah Rp84.000,00.
Jika Ibu membeli ikan tenggiri sebanyak 1 kilogram, maka total harga yang harus dibayar Ibu adalah …
- Rp126.000,00
- Rp138.000,00
- Rp147.000,00
- Rp152.000,00
- Rp165.000,00
Jawaban: C
Pembahasan:
Ubah bilangan campuran menjadi desimal:
1 = 1,75
Gunakan konsep perbandingan senilai (harga total = harga/kg × berat):
Total harga=84.000×1,75
Hitung:
84.000×1,75=84.000× = 84.000 × 1,75 = 147.000
Soal Nomor : 3
Kompetensi : Memahami, mengaplikasikan, dan bernalar yang lebih tinggi untuk menyelesaikan permasalahan terkait penentuan dan penaksiran rerata(mean), median, modus, dan jangkauan (range) dari data
Sebuah toko menjual telur dalam dua jenis kemasan. Kemasan Aberisi 8 butir telur dengan rata-rata berat 56 gram per butirdan kemasan B berisi 12 butir telur dengan rata-rata berat 60 gram per butir. Namun, setelah dilakukan penimbangan ulang, ditemukan bahwa 2 telur dari kemasan B rusak dan harus diganti dengan 2 telur dari kemasan A agar berat rata-rata dari gabungan kedua kemasan menjadi 57,5 gram per butir. Jika berat rata-rata telur yang tersisa di Kemasan A menjadi 54 gram per butir, tentukan berat rata-rata 2 telur yang dipindahkan dari Kemasan A ke Kemasan B!
- 45 gram
- 47,5 gram
- 50 gram
- 52 gram
- 55 gram
Jawaban: D
Pembahasan:
Langkah 1 — Tentukan total berat awal kedua kemasan
- Kemasan A: 8 × 56 = 448 gram
- Kemasan B: 12×60=720 gram
- Total awal = 448+720=1.168 gram
- Total telur = 8+12=20 butir
Langkah 2 — Setelah pemindahan telur
- Dari A → B: 2 telur (dengan rata-rata berat belum diketahui = x gram per telur)
- Berat Kemasan A berkurang 2x, dan sisa 6 telur di A sekarang rata-ratanya 54 g
→ berat sisa A = 6×54=324g
Maka berat awal A (448) = berat sisa (324) + berat yang dipindah (2x):
448 = 324 + 2x ⇒ 2x = 124 ⇒ x = 62
Jadi berat rata-rata 2 telur yang dipindahkan = 62 gram per butir
Namun, cek apakah ini konsisten dengan rata-rata total baru (57,5 g).
Langkah 3 — Uji konsistensi rata-rata gabungan
Sekarang komposisi setelah perubahan:
- A berisi 6 telur dengan total 324 g
- B berisi (12 − 2) + 2 = 12 telur
- 10 telur lama dari B = 10×60=600 g
- 2 telur baru dari A = 2 × 62 = 124 g
- Total B = 600+124=724 g
Total keseluruhan: 324 + 724 = 1.048 g
Jumlah telur: 6 + 12 = 18
Rata-rata gabungan baru = 1.048÷18≈58, 2 g → sedikit lebih besar dari 57,5 g.
Untuk rata-rata tepat 57,5, berarti berat telur yang dipindahkan harus sedikit lebih ringan dari 62 g. Mari hitung tepatnya
Langkah 4 — Hitung ulang berat ideal agar rata-rata tepat 57,5
Total berat yang diinginkan untuk 18 telur:
18 × 57,5 = 1.035 gram
Kita tahu:
- Berat sisa di A = 324 g
- Berat telur lama di B (10 butir) = 600 g
- Berat telur pindahan = 2x
324 + 600 + 2x = 1.035 ⇒ 2x = 111 ⇒ x = 55,5
Berat rata-rata 2 telur yang dipindahkan = 55,5 gram per butir.
Jawaban: D. 55 gram (mendekati 55,5 g)
Soal Nomor : 4
Kompetensi : Memahami, mengaplikasikan, dan bernalar yang lebih tinggi untuk menyelesaikan permasalahan terkait sistem persamaan linear dua variabel.
Misalkan ppp dan qqq merupakan bilangan real sehingga sistem persamaan linear berikut
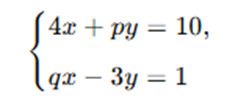
Mempunyai solusi (x, y) = (2,1)
Tentukan Benar atau Salah untuk setiap pernyataan berikut terkait dengan nilai a dan b!
| # | Pernyataan | Benar | Salah |
| A | (p = 3) | ||
| B | (q = 2) | ||
| C | (p + q = 5) | ||
| D | (p) dan (q) keduanya bilangan prima | ||
| E | Determinan sistem (D = -12 – pq) bernilai negatif |
Pembahasan:
Substitusi (x,y)=(2,1)(x, y) = (2, 1)(x,y)=(2,1) ke dalam kedua persamaan:
1️. Dari persamaan pertama:
4 (2) + p(1) = 10 ⇒8 + p = 10 ⇒ p = 2
2️. Dari persamaan kedua:
q(2) − 3 (1) = 1⇒ 2q – 3 = 1 ⇒ 2q = 4 ⇒ q = 2.
Jadi, diperoleh:
p=2, q = 2
Hitung determinan sistem:
D = 4 (−3)− pq = − 12 − (2)(2) = − 12 – 4 = − 16
→ D < 0
Kunci Jawaban dan Alasan
| No | Pernyataan | Jawaban | Alasan |
| A | (p = 3) | Salah | Karena (p = 2). |
| B | (q = 2) | Benar | Substitusi menghasilkan (q = 2). |
| C | (p + q = 5) | Salah | (p + q = 4). |
| D | (p) dan (q) keduanya bilangan prima | Benar | 2 adalah bilangan prima. |
| E | Determinan bernilai negative | Benar | (D = -16 < 0). |
Latihan Soal, Ayo Kerjakan!
Soal Nomor : 1
Kompetensi : Memahami, mengaplikasikan, dan bernalar yang lebih tinggi untuk menyelesaikan permasalahan terkait Faktorisasi prima bilangan asli
Terdapat tiga bilangan yang dinyatakan dengan:
(282−142), (202+ 300), dan (42×45)
Bilangan apa yang merupakan faktor persekutuan ketiga bilangan tersebut?
- 23 × 32 × 5
- 22 × 32 × 5
- 2 × 32 × 5
- 22 × 32
- 22 × 3 × 5
Soal Nomor : 2
Kompetensi : Memahami, mengaplikasikan, dan bernalar yang lebih tinggi untuk menyelesaikan permasalahan terkait perbandingan senilai dan berbalik nilai
Harga 1kilogram jeruk adalah Rp36.000,00.
Jika Rina membeli 2½ kilogram jeruk, maka total harga yang harus dibayar adalah …
- Rp72.000,00
- Rp81.000,00
- Rp85.000,00
- Rp90.000,00
- Rp93.000,00
Soal Nomor : 3
Kompetensi : Memahami, mengaplikasikan, dan bernalar yang lebih tinggi untuk menyelesaikan permasalahan terkait penentuan dan penaksiran rerata (mean), median, modus, dan jangkauan (range) dari data
Rata-rata berat telur kecil 45 gram, sedang 55 gram, besar 65 gram. Dalam satu kemasan terdapat 1 telur besar, 5 telur sedang, dan 2 telur kecil. Jika rata-rata berat telur dalam kemasan harus 55 gram, maka dua telur tambahan yang harus dipilih adalah ….
- 2 telur kecil
- 2 telur sedang
- 2 telur besar
- 1 telur besar dan 1 telur sedang
- 1 telur besar dan 1 telur kecil
Soal Nomor : 4
Kompetensi : Memahami, mengaplikasikan, dan bernalar yang lebih tinggi untuk menyelesaikan permasalahan terkait sistem persamaan linear dua variabel.
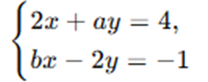
Mempunyai solusi (x,y) = (5,−2)
| # | Pernyataan | Benar | Salah |
| A | (a = 3) | ||
| B | (b = -1) | ||
| C | (10a + b = 31) | ||
| D | (a+b=2) | ||
| E | Determinan sistem bernilai nol |
Referensi:
Kementerian Pendidikan, Kebudayaan, Riset, dan Teknologi. (2023). Tes Kemampuan Akademik (TKA) – Panduan dan Kisi-Kisi Resmi. Pusat Asesmen Pendidikan (Pusmendik).
Pusmendik – Kemdikbudristek. (2023). Informasi Resmi Asesmen Nasional dan TKA SMP. Jakarta: Pusat Asesmen Pendidikan.




